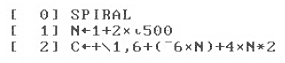Programming Challenge

by Charles Bovaird

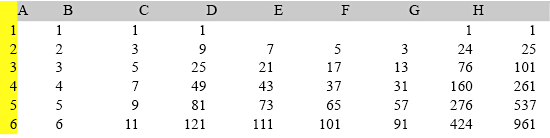
Problem number 1 –Solutions to the Spiral Matrix problem published in the
October 2007 DACSDOC

This is a continuation of the article in February 2008 DACSDOC on solutions to the spiral matrix problem.

A type (1) method - Written using a spreadsheet by Charles Bovaird (mathsig@dacs.org)

Description of Excel spreadsheet program - solution to the spiral matrix problem (first 7 rows)

The numeric values of each column represent the following:

If you duplicate the instructions your spreasdsheet should look like the following:

Method: Looking at the original problem matrix we observe there is one cell in the center surrounded by increasingly larger squares whose top right corner are 9 25 49 81 121…. These values are squares of the numbers 3 5 7 9 11…. We can now make a spreadsheet by placing in column A the values 1 2 3 4…. down to row 501. Using the spreadsheet cell pair drag and drop feature place in column B the values 1 3 5 7 9 etc to row 501. Column B values represent the number of cells that on the side of each square. In C1, D1, G1, and H1 enter a 1. In D2 code the function [=$B^2] and copy it down to row 501. These are the values of the top right corner of each square. Use columns D, E, and F to compute the remaining three corners of each square as an offset from column D. In column G2 sum the four corners [=SUM ($C2: $F2)] and copy it down the column to row 501. Type the function [=H1+G2] in cell H2 and copy it down to row 501. If you did it correctly the first six rows of your spreadsheet should look the same as above. The answer (669171001) to the problem lies in cell H501. Note: the center cell is not a square. The original problem definition clearly counted it as a 1 in the sum of the diagonals.

The same solution method can be quickly accomplished using the APL programming language as follows:

Line [ 1] puts a vector (string) of odd numbers from 3 to 1001 into variable N. (e.g 3 5 7 9…..997 999 1001). Line [ 2] puts a vector (string) of numbers containing the sum of the diagonals (e.g. 1 25 101 261 …. ) (see above spreadsheet) into variable C. The last (501st) number being 669171001. Typing C[501] would display 669171001.

A type (3) method – Algebraic solution enclosed in C++ code by David Wilkinson

BASIC ALGEBRA (based upon the odd numbers 1 3 5 ….. 999 1001)

The sum of the corner elements of a nxn spiral is 4*n*n -6*n + 6.
Writing n=2*m+1 gives 16*m*m + 4*m + 4.

So the sum of the diagonal terms in a NxN spiral is

1 + Sum_m (16*m*m +4*m + 4) (*)

where the sum runs from m=1 to m=M with N=2*M+1. To compute this you need to know

sum 1 = M
sum m = M*(M+1)/2
sum m*m = M*(M+1)*(2M+1)/6

where the sums run from m=1 to m=M.

Substituting these in (1 + Sum_m (16*m*m +4*m + 4)) gives

= 1 + 16*M*(M+1)*(2M+1)/6 + 4*M*(M+1)/2 + 4*M)
= 1 + M*(8*(M+1)*(2*M+1) + 6*(M+1) + 12)/3
= 1 + 2*M*(4*(M+1)*(2*M+1) + 3*(M+1) + 6)/3
= 1 + 2*M*( (8*M*M + 12*M + 4) + (3*M + 3) + 6)/3
= 1 + 2*M*(8*M*M + 15*M + 13)/3

where (to repeat), M is related to N by N=2*M

Students may wish to Google search with the argument "M*(M+1)*(2M+1)/6" (include quotes)..

This problem is easily soluble in closed form. These are the answers I get using the following C++
program, running on Visual C++ 6.0.

The C++ program, running on Visual C++ 6.0. (by Dave Wilkinson)
-----------------------------------------------------------------------
#include <iostream>
#include <iomanip>
using namespace std;
typedef unsigned int UINT;
> // return diagonal sum for (2n+1)-dimensional spiral
> UINT DiagSum(UINT n)
> {
> return 1 + 2*n*(8*n*n + 15*n +13)/3;
> }
>
> int main()
> {
> UINT a[5] = {0, 1, 2, 50, 500};
> for (int i=0; i<sizeof(a)/sizeof(a[0]); i++)
> {
> cout << setw(6) << 2*a[i] + 1 << setw(12) << DiagSum(a[i]) << "\n";
> }
> return 0;
> }